View Paper (Raw)

Q1. A resistance carries a current of 2 A . When its ends are connected to a copper wire, of negligible resistance, i.e. when it is short circuited, then current through it will be

1) 2 A

Q2. In the given figure,

(V_{1})

is

1)

(\frac{200}{3} V)

2)

(\frac{100}{3} V)

3)

(\frac{50}{3} V)

4) 50 V

Hint:

(V_{1}=iR R_{1}=(\frac{V}{R_{1}+R_{2}}) R_{1})

(( \frac{100}{25+50}) \times 25=\frac{100 \times 25}{75}=\frac{100}{3} V)

Q3. In the given figure, current through

(6 \Omega)

is

1) 1.5 A

2) 1.2 A

3) 0.8 A

4) 1.8 A

Hint: If

(i_{1})

be current in

(6 \Omega)

and

((i-i_{1}))

be current through

(9 \Omega)

.

(\therefore 6 i_{1}=9(i-i_{1}))

(6 i_{1}=9 i-9 i)

(15 i_{1}=9 \times 3)

(i_{1}=\frac{27}{15}=1.8 A)

Q4. In the given figure, applied voltage V is (All resistances are in

(\Omega)

)

1) 35 V

2) 45 V

3) 50 V

4) 55 V

Hint:

(V_{2}=V_{3})

(20 \times 0.5=10 \times i_{2})

(i_{2}=1 A)

(i=i_{1}+i_{2}=0.5+1=1.5 A)

(V_{1}=30 i=30 \times 1.5=45 V)

(V_{2}=20 \times 0.5=10 V)

(V=V_{1}+V_{2}=45+10=55 V)

Q5. Current through

(40 \Omega)

,

(60 \Omega)

and

(20 \Omega)

resistance, respectively

1) 6 A each

2) 2 A each

3)

(6 A, 4 A, 12 A)

4)

(12 A, 4 A, 6 A)

Hint: The circuit becomes

(i_{1}=\frac{240}{40}=6 A)

(i_{2}=\frac{240}{60}=4 A)

(i_{3}=\frac{240}{20}=12 A)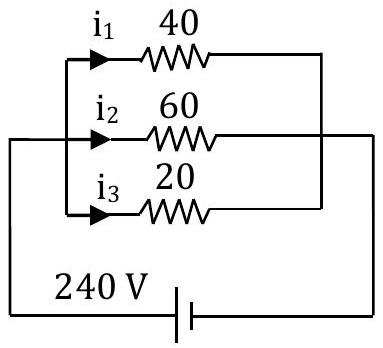

Q6. Two resistors,

(X)

and

(Y)

, having resistances

(R)

each, are connected in series across a potential difference

(V)

. When a resistance R is connected in parallel to Y , the percentage change in the potential difference across it will be

1)

(17 %)

2)

(25 %)

3)

(-17 %)

4)

(-25 %)

Hint:

\begin{aligned} & % \Delta V=\frac{\frac{V}{3}-\frac{V}{2}}{V} \times 100 \\ & =-\frac{V / 6}{V} \times 100=-\frac{100}{6}=-17 % \end{aligned}

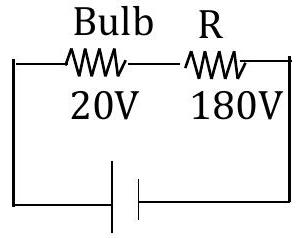
Q7. To use a bulb, rated at

(20 V, 6 W)

, with a 200 V source, you have to connect a resistance

1) in parallel with the bulb.

2) in series with the bulb.

3) in series or in parallel with the bulb.

4) none of the above

Hint: By connecting a resistance in series, 200 V gets divided into 2 parts, 20 V are as bulb and 180 V are as resistance. Diagram

Q8. In the accompanying circuit, if the resistance of

(R_{2})

is decreased, then

1) the current through

(R_{1})

increases.

2) the current through

(R_{1})

remains constant.

3) the voltage drop across

(R_{2})

decreases.

4) the power dissipated by

(R_{2})

decreases.

Q9. Three conductors draw currents of

(1 A, 2 A)

and 3 A respectively when connected in turn across a battery. If the series combination of them is connected across the same battery, the current drawn will be

1) 5 A

2) >1 A but < 2 A

3) < 1 A

4)

(\frac{5}{7} A)

Q10. If the current I in the given circuit is 0.1 A , then

(R=)

1)

(3 \Omega)

(30 \Omega)

2)

(30 \Omega)

3)

(60 \Omega)

4)

(300 \Omega)

Hint:

(R_{eff }=R||(R+R)=R|| 2 R=\frac{2 R}{3})

(R_{eff}=\frac{V}{I}=\frac{4}{0.1}=40 \Omega)

(\frac{2 R}{3}=40)

(R=\frac{40 \times 3}{2}=60 \Omega)

Q11. In the circuit shown below, the total resistance of the circuit between points

(P)

and

(Q)

is also equal to

(R)

. The value of the unknown resistor

(R)

is

1)

(3 \Omega)

2)

(\sqrt{39} \Omega)

3)

(\sqrt{69} \Omega)

4)

(10 \Omega)

Hint:

(R=3+\frac{10 \times(3+R)}{10+(3+R)})

(R-3=\frac{(30+10 R)}{(13+R)})

((R-3)(R+13)=10 R+30)

(R^{2}-3 R+13 R-39=10 R+30)

(R^{2}=69)

(\therefore R=\sqrt{69} \Omega)

Q12. The current through the

(4 \Omega)

resistor is

1) 0.5 A

2) 0.4 A

3) 3 A

4) 0.3 A

Hint:

(R_{eff }=[4||12]+2=3+2=5 \Omega)

(I=\frac{V}{R_{eff}}=\frac{2}{5}=0.4 A)

Voltage across

(4 \Omega)

is

(V_{1}=IR=0.4 \times 3=1.2 V)

(I_{1}=\frac{V_{1}}{R_{1}}=\frac{1.2}{4}=0.3 A)

Q13. Two resistors P and

(Q(P>Q))

are connected in series as shown in figure. With the usual symbols, which of the following is NOT true?

1)

(V_{AB}>V_{BC})

2)

(V_{C}

3)

(I_{1}=I_{2}=I_{3})

4)

(V_{B}>V_{A})

Hint: For series combination,

(I_{1}=I_{2}=I_{3})

As current flows from A to C ,

(V_{A}>V_{B}>V_{C})

(V_{AB}=I_{1} P)

(V_{BC}=I_{2} Q)

As

(P>Q)

and

(I_{1}=I_{2})

,

(V_{AB}>V_{BC})

Q14. Three voltmeters

(A, B)

and C having resistances

(R, \frac{3}{2} R)

and 3 R respectively are X - (A) connected as shown in the figure. When some potential difference is applied between X and Y , the respective voltmeter readings are

(V_{A}, V_{B})

and

(V_{C})

. Then

1)

(V_{A} \neq V_{B}=V_{C})

2)

(V_{A} \neq V_{B} \neq V_{C})

3)

(V_{A}=V_{B} \neq V_{C})

4)

(V_{A}=V_{B}=V_{C})

Hint:

(V_{A}=IR)

(V_{B}=\frac{2 I}{3} \times(\frac{3}{2} R)=IR)

(V_{C}=\frac{I}{3} \times(3 R)=IR)

(\therefore V_{A}=V_{B}=V_{C})

Paper Questions (Raw)