J J Science Academy - Practice Test

1) A resistance carries a current of 2 A . When its ends are connected to a copper wire, of negligible resistance, i.e. when it is short circuited, then current through it will be

1) 2 A

2) In the given figure, $V_{1}$ is

1) $\frac{200}{3} V$
2) $\frac{100}{3} V$
3) $\frac{50}{3} V$
4) 50 V

Hint: $V_{1}=iR R_{1}=(\frac{V}{R_{1}+R_{2}}) R_{1}$ $( (\frac{100}{25+50}) \times 25=\frac{100 \times 25}{75}=\frac{100}{3} V)$

3) In the given figure, current through $6 \Omega$ is

1) 1.5 A
2) 1.2 A
3) 0.8 A
4) 1.8 A

Hint: If $i_{1}$ be current in $6 \Omega$ and $(i-i_{1})$ be current through $9 \Omega$. $\therefore 6 i_{1}=9(i-i_{1})$ $(6 i_{1}=9 i-9 i)$ $(15 i_{1}=9 \times 3)$ $(i_{1}=\frac{27}{15}=1.8 A)$

4) In the given figure, applied voltage V is (All resistances are in $\Omega$ )

1) 35 V
2) 45 V
3) 50 V
4) 55 V

Hint: $V_{2}=V_{3}$ $(20 \times 0.5=10 \times i_{2})$ $(i_{2}=1 A)$ $(i=i_{1}+i_{2}=0.5+1=1.5 A)$ $(V_{1}=30 i=30 \times 1.5=45 V)$ $(V_{2}=20 \times 0.5=10 V)$ $(V=V_{1}+V_{2}=45+10=55 V)$

5) Current through $40 \Omega$, $60 \Omega$ and $20 \Omega$ resistance, respectively

1) 6 A each
2) 2 A each
3) $6 A, 4 A, 12 A$
4) $12 A, 4 A, 6 A$

Hint: The circuit becomes $i_{1}=\frac{240}{40}=6 A$ $i_{2}=\frac{240}{60}=4 A$ $i_{3}=\frac{240}{20}=12 A$ 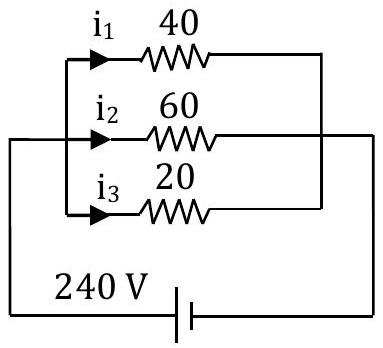Diagram

6) Two resistors, $X$ and $Y$, having resistances $R$ each, are connected in series across a potential difference $V$. When a resistance R is connected in parallel to Y , the percentage change in the potential difference across it will be

1) $17 \%$
2) $25 \%$
3) $-17 \%$
4) $-25 \%$

Hint: $$ \begin{aligned} & % \Delta V=\frac{\frac{V}{3}-\frac{V}{2}}{V} \times 100 \\ & =-\frac{V / 6}{V} \times 100=-\frac{100}{6}=-17 % \end{aligned} $$

7) To use a bulb, rated at $20 V, 6 W$, with a 200 V source, you have to connect a resistance

1) in parallel with the bulb.
2) in series with the bulb.
3) in series or in parallel with the bulb.
4) none of the above

Hint: By connecting a resistance in series, 200 V gets divided into 2 parts, 20 V are as bulb and 180 V are as resistance. 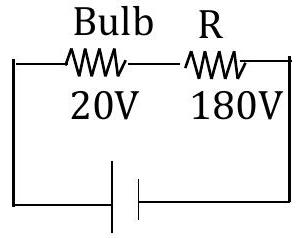Diagram

8) In the accompanying circuit, if the resistance of $R_{2}$ is decreased, then

1) the current through $R_{1}$ increases.
2) the current through $R_{1}$ remains constant.
3) the voltage drop across $R_{2}$ decreases.
4) the power dissipated by $R_{2}$ decreases.

9) Three conductors draw currents of $1 A, 2 A$ and 3 A respectively when connected in turn across a battery. If the series combination of them is connected across the same battery, the current drawn will be

1) 5 A
2) >1 A but < 2 A
3) < 1 A
4) $\frac{5}{7} A$

10) If the current I in the given circuit is 0.1 A , then $R=$

1) $3 \Omega$ $30 \Omega$
2) $30 \Omega$
3) $60 \Omega$
4) $300 \Omega$

Hint: $R_{eff }=R||(R+R)=R|| 2 R=\frac{2 R}{3}$ $(R_{eff}=\frac{V}{I}=\frac{4}{0.1}=40 \Omega)$ $(\frac{2 R}{3}=40)$ $(R=\frac{40 \times 3}{2}=60 \Omega)$

11) In the circuit shown below, the total resistance of the circuit between points $P$ and $Q$ is also equal to $R$. The value of the unknown resistor $R$ is

1) $3 \Omega$
2) $\sqrt{39} \Omega$
3) $\sqrt{69} \Omega$
4) $10 \Omega$

Hint: $R=3+\frac{10 \times(3+R)}{10+(3+R)}$ $(R-3=\frac{(30+10 R)}{(13+R)})$ $((R-3)(R+13)=10 R+30)$ $(R^{2}-3 R+13 R-39=10 R+30)$ $(R^{2}=69)$ $(\therefore R=\sqrt{69} \Omega)$

12) The current through the $4 \Omega$ resistor is

1) 0.5 A
2) 0.4 A
3) 3 A
4) 0.3 A

Hint: $R_{eff }=[4||12]+2=3+2=5 \Omega$ $(I=\frac{V}{R_{eff}}=\frac{2}{5}=0.4 A)$ Voltage across $4 \Omega$ is $(V_{1}=IR=0.4 \times 3=1.2 V)$ $(I_{1}=\frac{V_{1}}{R_{1}}=\frac{1.2}{4}=0.3 A)$

13) Two resistors P and $Q(P>Q)$ are connected in series as shown in figure. With the usual symbols, which of the following is NOT true?

1) $V_{AB}>V_{BC}$
2) $V_{C}
3) $I_{1}=I_{2}=I_{3}$
4) $V_{B}>V_{A}$

Hint: For series combination, $I_{1}=I_{2}=I_{3}$ As current flows from A to C , $V_{A}>V_{B}>V_{C}$ $V_{AB}=I_{1} P$ $V_{BC}=I_{2} Q$ As $(P>Q)$ and $(I_{1}=I_{2})$, $V_{AB}>V_{BC}$

14) Three voltmeters $A, B$ and C having resistances $R, \frac{3}{2} R$ and 3 R respectively are X - (A) connected as shown in the figure. When some potential difference is applied between X and Y , the respective voltmeter readings are $V_{A}, V_{B}$ and $V_{C}$. Then

1) $V_{A} \neq V_{B}=V_{C}$
2) $V_{A} \neq V_{B} \neq V_{C}$
3) $V_{A}=V_{B} \neq V_{C}$
4) $V_{A}=V_{B}=V_{C}$

Hint: $V_{A}=IR$ $(V_{B}=\frac{2 I}{3} \times(\frac{3}{2} R)=IR)$ $(V_{C}=\frac{I}{3} \times(3 R)=IR)$ $(\therefore V_{A}=V_{B}=V_{C})$