Paper Questions (Raw)
Q1. Resistance between A and B in the given circuit is (all resistances are in ($\Omega$))
1) ($10 \Omega$)
2) ($20 \Omega$)
3) ($40 \Omega$)
4) ($\frac{20}{3} \Omega$)
Hint: ($R_1=10+20=30 \Omega$)($R_2=30 \| 30=15 \Omega$)($R_3=25+15=40 \Omega$)($R_4=40 \| 40=20 \Omega$)($R_{AB}=20 \| 20=10 \Omega$)
Q2. Resistance between A and B in the given circuit is (all resistances are in ($\Omega$))
1) ($\frac{1}{2} \Omega$)
2) ($1 \Omega$)
3) ($2 \Omega$)
4) ($4 \Omega$)
Hint: ($R_1=4+4=8 \Omega$)($R_2=5+3=8 \Omega$)($R_3=8 \| 4 \| 8=2 \Omega$)($R_{AB}=2 \| 2=1 \Omega$)
Q3. 10 resistances, each of value R , are connected in parallel to give ($20 \Omega$). Now they are connected as shown in the figure. The resistance between ($A$) and ($B$) is
1) ($\frac{140}{3} \Omega$)
2) ($\frac{540}{7} \Omega$)
3) ($\frac{1100}{9} \Omega$)
4) ($\frac{620}{3} \Omega$)
Hint: When they are connected in parallel,
$$ \frac{R}{10}=20 \Omega $$
($R=200 \Omega$)Refer diagram,
$$ \begin{aligned} R_{AC} & =\frac{R}{3}=\frac{200}{3} \Omega \\ R_{CD} & =\frac{R}{2}=\frac{200}{2}=100 \Omega \\ R_{DB} & =\frac{R}{2}=\frac{200}{5}=40 \Omega \\ R_{AB} & =R_{AC}+R_{CD}+R_{DB}=\frac{200}{3}+100+40 \\ & =\frac{200}{3}+140=\frac{200+420}{3}=\frac{620}{3} \Omega \end{aligned} $$
Q4. In the given figure, the slider contact, of rheostat ($R_h$), is at a distance of (($\frac{2}{3}$)$^{rd}$) the length of rheostat from C . Resistance between A and B is
1) ($\frac{40}{3} \Omega$)
2) ($\frac{80}{3} \Omega$)
3) ($40 \Omega$)
4) ($80 \Omega$)
Hint: ($\ell_{CE}=\frac{2}{3} \ell_{CD}$)($R_{CE}=\frac{2}{3} R_{CD}=\frac{2}{3} \times 36=24 \Omega$)($R_{ACEF}=6+24+12+8=50 \Omega$)($R_{AB}=50 \| 200=\frac{200}{5}=40 \Omega$)
Q5. In the given figure, when ($K_1$), is closed ($R_{AB}=R_1$) and when ($K_2$) is closed, ($R_{AB}=R_2$). Then, ($\frac{R_1}{R_2}=$)
1) ($\frac{8}{5}$)
2) ($\frac{3}{1}$)
3) ($\frac{20}{13}$)
4) ($\frac{13}{20}$)
Hint: When
($K_1$) is closed, the circuit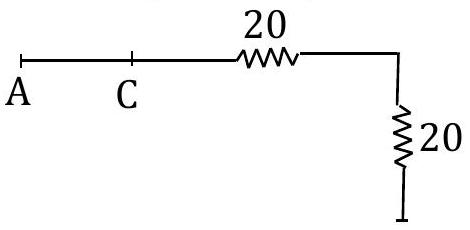
($60 \| 30=\frac{60}{3}=20 \Omega^B$)($R_{AB}=R_1=20+20=40 \Omega$)When
($K_2$) is closed, the circuit
$$
\begin{figure}
\includegraphics[max width=\textwidth]{https://cdn.mathpix.com/cropped/e65ca676-ffec-4646-81fa-f098ea31debc-4.jpg?height=254&width=467&top_left_y=169&top_left_x=123}
\captionsetup{labelformat=empty}
\caption{R_{AB}=R_{2}=6+20=26 \Omega}
\end{figure}
$$
($R_{AB}=R_2=6+20=26 \Omega$)($\therefore \frac{R_1}{R_2}=\frac{40}{26}=\frac{20}{13}$)
Q6. The total resistance across ($A$) and ($B$) in the circuit figure is
1) ($2 R$)
2) ($\frac{2 R}{3}$)
3) ($\frac{R}{2}$)
4) ($\frac{R}{3}$)
Hint: Apply laws of resistances starting from the resistance between D and F .($R_1=R+R=2R$)($R_2=2R \| 2R \| R=R / 2$)($R_3=\frac{R}{2}+\frac{R}{2}=R$)($R_{AB}=R \| R=R / 2$)
Q7. Two metal wires of identical dimensions are connected in series. If ' ($\sigma_1$) ' and ' ($\sigma_2$) ' are the conductivities of the metals respectively, then the effective conductivity of the combination is
1) ($\sigma_1+\sigma_2$)
2) ($\frac{\sigma_1+\sigma_2}{2}$)
3) ($\frac{\sigma_1 \sigma_2}{\sigma_1+\sigma_2}$)
4) ($\frac{2 \sigma_1 \sigma_2}{\sigma_1+\sigma_2}$)
Hint: ($R=\frac{\rho \ell}{A}=\frac{\ell}{\sigma A}$)($\therefore R_S=R_1+R_2$)($\frac{2 \ell}{\sigma_S A}=\frac{\ell}{\sigma_1 A}+\frac{\ell}{\sigma_2 A}$)($\frac{2}{\sigma_S}=\frac{1}{\sigma_1}+\frac{1}{\sigma_2}=\frac{\sigma_2+\sigma_1}{\sigma_1 \sigma_2}$)($\sigma_S=\frac{2 \sigma_1 \sigma_2}{\sigma_1+\sigma_2}$)
Q8. A metallic wire of length ($L$) and cross-section A has a resistance ($36 \Omega$). Two wires of the same material, length ($2 L$) and cross-section 3A are connected in series. The combination has a resistance of
1) ($24 \Omega$)
2) ($36 \Omega$)
3) ($48 \Omega$)
4) ($108 \Omega$)
Hint: ($R=\frac{\rho L}{A}=36 \Omega$)($R'=\frac{\rho(2L)}{(3A)}=\frac{2}{3}\times36=24\Omega$)($R = R' + R'=24 + 24=48 \Omega$)
Q9. A technician has only two resistance coils. By using them singly, in series or in parallel, he is able to obtain the resistance ($3 \Omega$), ($4 \Omega$), ($12 \Omega$) and ($16 \Omega$). The resistances of two coils are
1) ($6 \Omega$) and ($10\Omega$)
2) ($4 \Omega$) and ($12 \Omega$)
3) ($7 \Omega$) and ($9 \Omega$)
4) ($4 \Omega$) and ($16 \Omega$)
Q10. The equivalent resistance in series combination is
1) lower than the highest resistance.
2) higher than the highest resistance.
3) lower than the lowest resistance.
4) higher than the lowest resistance.
Q11. A resistor of ($0.5 \Omega$) is connected to another resistor, in parallel combination, to get an equivalent resistance of ($0.1 \Omega$). The resistance of second resistor is
1) ($8 \Omega$)
2) ($\frac{1}{8} \Omega$)
3) ($\frac{1}{12} \Omega$)
4) ($12 \Omega$)
Hint: ($\frac{1}{R'}=\frac{1}{R}+\frac{1}{0.5}=\frac{0.5+R}{(0.5) R}$)($R'=\frac{(0.5) R}{0.5+R}=0.1 \Omega$)($0.5 R=0.05+0.1 R$)($0.4 R=0.05$)($R=\frac{5}{40}=\frac{1}{8} \Omega$)